0.1.1 Computación: Máquina de Turing
"... ¿Qué significa esto en lo que se refiere al universo físico? La respuesta de Wheeler a esta pregunta es tan asombrosa como profunda. Concluye que ya no podemos seguir considerando el universo como un hardware que existe "ahí fuera", sino que debemos empezar a verlo como compuesto por un "software 'significativo'" y situado, como dice Wheeler, "quién sabe dónde". En otras palabras, hemos empezado a ver el universo como constituido en definitiva no por materia y energía, sino por pura información". Michael Talbot. "Mas allá de la Teoría Cuántica". Edit. Gedisa 3ª Edición 1995 Barcelona.
§1 Presentación
Encontra de lo que pudiera parecer, la ciencia de la computación y las teorías sobre computabilidad no pertenecen a la disciplina que hoy conocemos como "Informática", sino a las matemáticas, que son, con mucho, anteriores a aquella.
A principio del siglo XX, el campo de la matemática teórica estaba en plena efervescencia, gracias sobre todo a los trabajos de Hilbert y Gödel. En particular Hilbert había planteado ciertas cuestiones que derivaron en las teorías de la computación y la computabilidad, en concreto cual sería el significado de la computabilidad de un procedimiento.
En matemáticas se considera que un método o procedimiento es efectivo para obtener un resultado cuando se cumple que:
- El procedimiento puede ser expresado mediante un algoritmo (un número finito de instrucciones
concretas
 1.2.1); en el que cada instrucción puede ser expresada por un número
finito de símbolos.
1.2.1); en el que cada instrucción puede ser expresada por un número
finito de símbolos. - El procedimiento puede ser seguido sin error para conseguir el resultado en un número finito de pasos.
- El procedimiento puede ser (al menos teóricamente) seguido por un humano sin más ayuda que un papel y lápiz.
- El procedimiento no exige ninguna habilidad o inteligencia especial por parte de la persona que lo ejecuta. En lenguaje coloquial diríamos que "hasta un tonto podría hacerlo". La idea es que solo haya que seguir ciertas reglas de forma mecánica. Por esta razón cuando se cumplen estas condiciones se dice que el procedimiento es efectivo o "mecánico".
Para dar una definición matemáticamente precisa de lo que es un algoritmo,
Turing ideó un dispositivo imaginario al que denominó Máquina de
computación lógica LCM ("Logical Computing Machine"), pero que ha recibido en su honor el nombre
de máquina de Turing. Aunque su propuesta es anterior a la aparición de los computadores digitales (1936
"On computable numbers, with an application to the Entscheidungproblem"), actualmente
es el objeto central de estudio de los teóricos de la computación.
Precisamente la definición moderna de lo que es "Computable" se
basa en este concepto, y del mismo modo que cuando se habla de inteligencia artificial es inevitable
referirse al Test de Turing, cuando se habla de algoritmos y computación es casi inevitable encontrar alguna
referencia a la máquina de Turing [1]. Por si esto fuera poco, los
conceptos subyacentes en la idea han jugado un papel importante en las recientes teorías filosóficas sobre la mente.
Lo que confiere al dispositivo su extraordinaria importancia es que es capaz de resolver cualquier problema matemático a condición de que haya sido reducido a un algoritmo.
Nota: Una buena introducción al tema en la Enciclopedia Stanford de Filosofía: Hodges, Andrew,
"Alan Turing" ![]() plato.stanford.edu.
plato.stanford.edu.
§2 La máquina de Turing
Una máquina de Turing es un autómata que se mueve sobre una secuencia lineal de datos. En cada instante la máquina puede leer un solo dato de la secuencia (generalmente un carácter) y realiza ciertas acciones en base a una tabla que tiene en cuenta su "estado" actual (interno) y el último dato leído. Entre las acciones está la posibilidad de escribir nuevos datos en la secuencia; recorrer la secuencia en ambos sentidos y cambiar de "estado" dentro de un conjunto finito de estados posibles.
En realidad la máquina de Turing es más una abstracción matemática que un dispositivo físico o mecánico. El hecho que se le denomine "máquina" se debe a que su funcionamiento puede ser descrito en términos de operaciones individuales muy sencillas que sugieren una implementación real muy simple, lo que ha motivado que existan muchas versiones prácticas del mismo.
Existen diversas "variedades" de una máquina de Turing, pero la más simple puede ser descrita diciendo que es cualquier dispositivo que cumple las siguientes condiciones:
-
Tiene una cinta sobre la que puede desplazarse a izquierda y derecha un cabezal de lectura/escritura. La cinta contiene una serie de celdas, y en cada una de ellas puede escribirse un símbolo de un conjunto finito; este conjunto de símbolos se denomina el alfabeto de la máquina [2]. En principio todas las celdas que no se hayan escrito antes contienen un carácter especial nulo o vacío (que se representa por 0 o #). La cinta puede contener tantas celdas a derecha e izquierda del cabezal como sean necesarias para el funcionamiento de la máquina.
-
El cabezal puede moverse a derecha (R) a izquierda (L) de su posición actual, así como leer el contenido de una celda o escribir en ella cualquier carácter de su alfabeto.
-
Existe un registro de estado que almacena el estado de la máquina. El número de estados posibles es finito, y no se exige ningún estado especial con el que sea iniciada la máquina.
-
Existe una tabla de acción [3], que contiene las instrucciones de lo que hará el autómata. Estas instrucciones representan en cierta forma el "programa" de la máquina. Las ejecución de cada instrucción de la tabla de acción incluye cuatro pasos:
Leer un carácter en la posición actual.
Escribir un nuevo símbolo en esta posición (puede ser el mismo que había). El símbolo a escribir es alguno del alfabeto de la máquina, y depende del carácter leído y del estado actual.
Desplazar el cabezal una celda a derecha o izquierda (R/L); en algunos modelos el desplazamiento puede ser nulo (detener H).
Decidir cual será el nuevo estado en función del carácter que se acaba de leer y del estado actual. Si la tabla de acción no contiene ninguna correspondencia con el estado actual y el símbolo leído, entonces la máquina detiene su funcionamiento.
En los modelos didácticos computarizados [5] la tabla suele definirse mediante
una matriz de cinco columnas que contiene:
Estado/Carácter-leído/Carácter-a-escribir/Movimiento/Nuevo-estado
|
+---+---++---+---+---+ | S | R || W | M | N | +---+---++---+---+---+ | 0 | 0 || 0 | R | 0 | | 0 | 1 || 1 | R | 1 | | 1 | 0 || 1 | R | 2 | | 1 | 1 || 1 | R | 1 | | 2 | 0 || 0 | H | 2 | | 2 | 1 || 0 | H | 2 | +---+---++---+---+---+ S = Estado actual R = Carácter leído W = Carácter escrito M = Dirección del movimiento N = Nuevo estado |
En el recuadro se incluye una muestra de una de estas tablas. Representa el comportamiento de una máquina de turing
que es capaz de sumar 1 a cualquier número unario (![]() 0.1). El alfabeto solo tiene dos símbolos: Vacío (0) y valor (1). La
máquina puede adoptar tres estados diferentes numerados del 0 al 2 (es costumbre señalar el estado inicial con 0). El
movimiento H ("Halt") significa no desplazar el cabezal. En este caso la máquina se detiene (o entra en un
bucle sin fin).
0.1). El alfabeto solo tiene dos símbolos: Vacío (0) y valor (1). La
máquina puede adoptar tres estados diferentes numerados del 0 al 2 (es costumbre señalar el estado inicial con 0). El
movimiento H ("Halt") significa no desplazar el cabezal. En este caso la máquina se detiene (o entra en un
bucle sin fin).
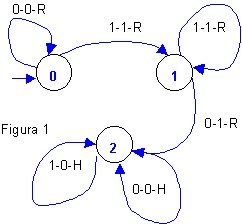 |
También es posible representar la tabla de acción mediante un grafo. Los diferentes estados internos se representan por círculos. Los cambios de estado con flechas a las que se añade una leyenda. Generalmente se utiliza una flecha para señalar el estado inicial. En la figura 1 se muestra el grafo correspondiente a la tabla.
Es notable que el diseño de Turing contiene de forma implícita la idea de que el autómata puede alterar su propio programa, pero el punto más significativo de su filosofía de funcionamiento es que se comporta como la mente, en el sentido que la configuración interna de la máquina establece el entorno en el que se toman las decisiones, de forma que la acción depende de dos factores: el estado interno y la información externa que puede "ver" a través de su cabezal [6]. La consecuencia es que es imposible predecir su comportamiento de la simple inspección de su tabla de acción, ya que el comportamiento depende también de la entrada recibida.
El hecho que el número de estados posibles y su alfabeto sea finitos, califica a estos autómatas como máquinas de estados finitos FSM ("Finite State Machine").
Nota: algunos teóricos sostienen que la genuina máquina de Turing solo utiliza un alfabeto unario, mientras que una máquina de estados finitos es más general y puede utilizar un alfabeto con más símbolos.
Es significativo que la cinta puede extenderse indefinidamente a derecha e izquierda, lo que hace que en la
práctica sea imposible construir un modelo real de lo que se denomina un sistema de Turing completo (ver a continuación
§4 ![]() ).
Es también destacable que la máquina da a la cinta tres utilizaciones distintas:
).
Es también destacable que la máquina da a la cinta tres utilizaciones distintas:
- Como elemento de almacenamiento de los datos de entrada (de capacidad potencialmente ilimitada)
- Como elemento de salida (de cualquier cantidad de datos)
- Como almacenamiento de información intermedia durante el proceso (puede ser de cualquier tamaño).
Aunque tanto el alfabeto utilizado como el número de estados son finitos, lo que confiere su potencia a la máquina de Turing (además de su diseño genial) es su almacenamiento ilimitado. Turing probó que este autómata es también un computador universal. Es decir, que puede emular el comportamiento de cualquier dispositivo cuyo comportamiento pueda ser expresado simbólicamente mediante un algoritmo.
§3 Ejemplo
R: Símbolo leído W: Símbolo a escribir M: Movimiento (R, L). N: Nuevo estado. |
Supongamos una máquina de Turing con un alfabeto unario, en la que el nulo (ausencia de dato) lo señalamos con 0. La máquina puede tener cinco estados que denominamos {e0, e1, e2, e3, e4}. El estado inicial es e0; su tabla de acción se muestra a la derecha.
Observe que la tabla debe contener al menos tantas filas como estados distintos. La primera columna representa lo que podíamos denominar "estado mental" de la máquina. La segunda columna indica el carácter leído; representa la entrada (input) al autómata. Las siguientes (en otro color) representan el comportamiento o respuesta de la máquina para la combinación estado/carácter-leído. Esta respuesta tiene tres componentes:
- Una salida (escribir en la cinta). Indicado en la columna W.
- Un movimiento de avance o retroceso del cabezal sobre la cinta (indicado en la columna M).
- Un cambio del estado interno actual del autómata a otro nuevo (columna N).
Observe que las filas pueden repetir el primer elemento; significan las acciones a tomar en cada estado según el carácter leído. Cada vez que se alcanza un estado para el que no exista una entrada para el carácter leído, la máquina se detiene. En nuestro autómata la tabla señala acciones concretas para cualquier carácter leído (0 o 1) en cualquiera de los estados e1, e2, e3 y e4, pero si en el estado e0 se lee un 0, la máquina se detiene.
La sucesión de pasos de cómputo es la siguiente (suponemos un estado inicial cualquiera ex):
1.- Se lee un carácter c (en nuestro caso es necesariamente 0 o 1)
2.- Se mira en la tabla que fila corresponde a la combinación ex/c.
3a.- Si no existe entrada la máquina se detiene.
3b.- Si existe entrada se ejecuta la instrucción (columnas en marrón claro) en el siguiente orden:
3b1.- Se escribe en la posición actual el carácter señalado (puede ser el mismo que había).
3b2.- Se mueve el cabezal una posición a izquierda o derecha.
3b3.- Se pasa al estado señalado en la última columna (puede implicar no cambiar de estado).
3b4.- Se repite el ciclo desde el punto 1.
Un ejemplo concreto debe comenzar en un estado determinado y con una cinta que contenga cualquier conjunto no nulo de
caracteres del alfabeto del autómata. El autómata de nuestro ejemplo [4] espera estar situado en el
primer carácter (izquierdo) de una cantidad cualquiera representada en unario
(![]() 0.1). El
programa hace que el autómata lea la cantidad y la repita a la derecha separadas por un nulo (0). Por ejemplo, si encuentra 111100000 lo transforma en 111101111.
0.1). El
programa hace que el autómata lea la cantidad y la repita a la derecha separadas por un nulo (0). Por ejemplo, si encuentra 111100000 lo transforma en 111101111.
Un ejemplo del proceso de esta máquina puede ser el que se muestra a continuación. Como el número de pasos de cómputo hasta que la máquina se detiene, depende de la cantidad inicial representada en la cinta, para hacer el ciclo más breve supondremos que hay un 2 (110000...). Los pasos ejecutados por el autómata para realizar el proceso se muestran en la tabla inferior. La información contenida en la cinta para cada paso es la existente "antes" de la ejecución del ciclo correspondiente. El carácter en negrita indica la posición de la cabeza en el momento de la lectura.
| |||||||||||||||||||||||||||||||||||||||||||||||||||
P1: La máquina ejecuta el primer paso. Arranca en el estado e0, donde lee un
1; entonces, de acuerdo con su tabla de acción escribe un 0 en esa posición, se
mueve a la derecha y entra en estado e1.
P2: En e1 lee un 1, escribe un 1 y se mueve a la derecha. Sigue en e1.
P3: En e1 lee 0, escribe 0, se mueve a la derecha y cambia a e2
P4: En e2 lee 0, escribe 1, se mueve a la izquierda y cambia a e3
P5: En e3 lee 0, escribe 0, se mueve a la izquierda y cambia a e4
P6: En e4 lee 1, escribe 1, se mueve a la izquierda y sigue en e4
El proceso sigue la misma lógica a través de los sucesivos pasos hasta llegar al último.
P15: En e0 lee 0; no existe ninguna entrada en la tabla para esta combinación, por lo que el autómata se detiene. Comprobamos como al final ha escrito en la cinta la cantidad esperada: 11011.
§3 Sistema de Turing completo
Un sistema Turing completo es aquel que puede simular el comportamiento de una máquina de Turing. Es evidente que salvando los problemas de memoria, los ordenadores modernos y los lenguajes de programación de uso general, son sistemas de Turing completos. También es evidente, que con independencia de su forma concreta, cualquier dispositivo que se comporte como un sistema de Turing completo, puede en principio ejecutar cualquier cálculo que realice cualquier computador.
Nota: Observe que la anterior afirmación no menciona para nada la posible dificultad de escribir el programa o del tiempo que pueda emplear en realizar el cálculo (cualquier cálculo que pueda hacer un ordenador puede teóricamente efectuarse con papel y lápiz).
§4 Recursos Web
La información que puede encontrarse sobre estas cuestiones en la Red es muy
abundante. Apate de la página de Andrew Hodge sobre Turing señalada en
la nota ![]() , señalaría estas:
, señalaría estas:
- Copeland, B. Jack, "The Modern History of Computing"

plato.stanford.edu.
En esta página de la Stanford Encyclopedia of Philosophy puede obtenerse una amplia descripción sobre los orígenes e historia de la computación.
- Página dedicada a la máquina de Turing del CSLI
 www-csli.stanford.edu
www-csli.stanford.edu
El CSLI ("Center for the Study of Language and Information") es un centro de investigación independiente fundado en 1983 por investigadores de la universidad de Stanford en California, de SRI International y del legendario Xerox PARC.
Existen diversos programas que permiten simular y observar el comportamiento de uno de estos autómatas en un PC. Como además de la informática, el tema pertenece al ámbito de la matemática teórica, generalmente han sido desarrollados por profesores de esta materia. Una característica general es que permiten ejecutar la computación a diversas velocidades seleccionables por el usuario o paso a paso. A continuación se relacionan algunos de los más interesantes.
- Visual Turing
 www.cheransoft.com
Página mantenida por Cristian Cheran (Cheran Software)
www.cheransoft.com
Página mantenida por Cristian Cheran (Cheran Software)
Visual Turing es un programa Windows (95, 98, NT, 2000) que permite experimentar con máquinas de Turing. Dispone de una avanzada interfaz gráfica que permite cortar, copiar y pegar. Se pueden ver las variables; permite la ejecución paso a paso y deshacer la última instrucción ("Undo").
- xTuringMachine Lab
 math.hws.edu
math.hws.edu
El programa anterior puede resultar sin duda muy avanzado para el principiante, de forma que para empezar quizás sea más recomendable utilizar este simulador de David J. Eck, del Departamento de Matemáticas y Ciencia de la computación en Hobart and William Smith Colleges. Es un applet Java que incluye un extenso comentario y diversos ejercicios. También puede ser reprogramado para realizar nuestros propios modelos.
- JKTuring
 homepage.smc.edu
homepage.smc.edu
Este programa de John Kennedy, del departamento de matemáticas del Santa Monica College en California, es un simulador FSM para Windows. El autor presenta además una interesante colección de programas para el aprendizaje de las matemáticas.
[1] El Test de Turing y la
máquina de Turing se refieren a conceptos distintos, aunque ambos ostentan el
nombre de Alan Mathison Turing. Famoso matemático inglés (1912-1954)
cuyas contribuciones en el campo de la matemática y de la teoría de la
computación le han valido ser considerado uno de los padres de la computación
digital. Alan Turing home page ![]() www.turing.org.uk
www.turing.org.uk
[2] Esta cinta es la representación de una memoria. En los ordenadores digitales binarios el alfabeto solo tiene dos símbolos representados por el '0' y el '1'. Dentro de las limitaciones de memoria, un ordenador digital moderno es una máquina de Turing.
[3] En el ordenador digital la tabla de acción está representada por el programa.
[4] Ejemplo tomado de Wikipedia ("The free Encyclopedia")
![]() www.wikipedia.org.
Publicado bajo las condiciones de la "GNU Free Documentation License".
www.wikipedia.org.
Publicado bajo las condiciones de la "GNU Free Documentation License".
[5] Son los más frecuentes (ver referencias Web
![]() ),
pero se han construido también modelos mecánicos, en cuyo caso la tabla de
acción puede estar representada de otra forma.
),
pero se han construido también modelos mecánicos, en cuyo caso la tabla de
acción puede estar representada de otra forma.
[6] El contenido de la "vantana", representado por los caracteres que pasan delante del cabezal de lectura, es lo que se denomina universo de Turing.